A simple example illustrates the greedy approach. Joe, the sales clerk, often encounters the problem of giving change for a purchase. Customers usually don’t want to receive a lot of coins. For example, most customers would be aggravated if he gave them 87 pennies when the change was $0.87. Therefore, his goal is not only to give the correct change, but to do so with as few coins as possible.

정확하게 거스름돈을 건네주면서 가능한 코인을 적게 주는 것이 이 문제의 핵심이다.

보통의 고객은 잔돈으로 많은 동전을 받기를 꺼려한다는 점을 상기하자. 잔돈을 거슬러주거나 받을 때 우리는 무의식적으로 탐욕적인 방법을 이미 사용하고 있다.

Example A greedy algorithm for giving change. The amount owed is 36 cents.

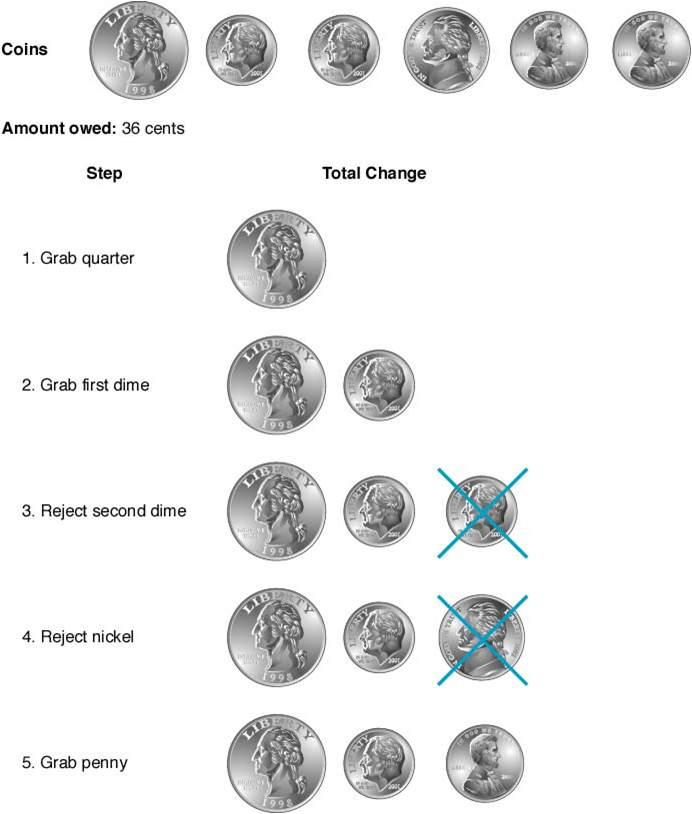
위의 그림은 주어진 문제에 대하여 탐욕적인 접근 방법을 잘 보여주고 있다. 36센트를 맞춰야 하므로 먼저 가장 큰 25센트를, 그 다음엔 10센트를, 마지막으로 1센트를 잡음으로써 최적의 해답에 도달한다. (￠36 = ￠25 ＋ ￠10 ＋ ￠1)

Example The greedy algorithm is not optimal if a 12-cent coin is included. The amount owed is 16 cents.

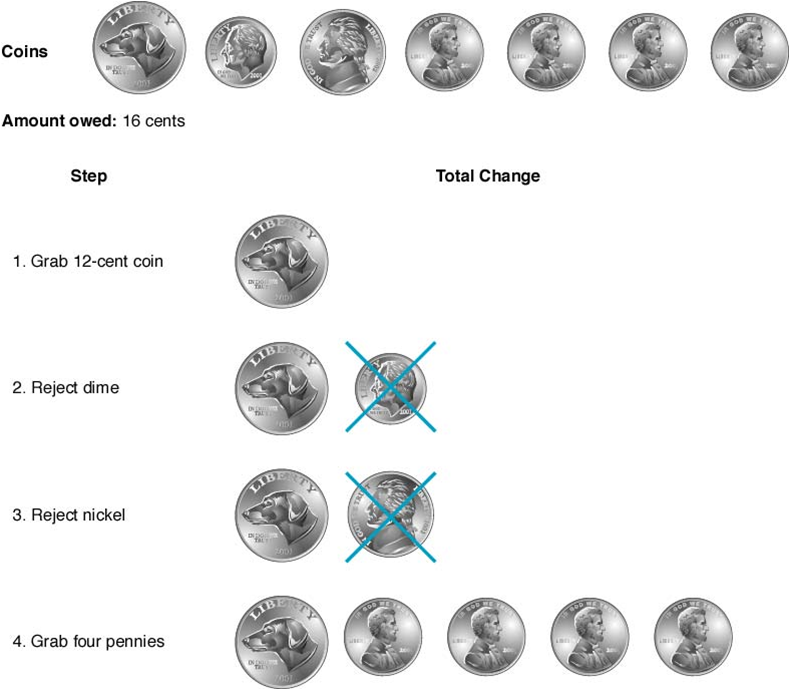
12센트짜리가 포함된 상태로 16센트를 거슬러줘야 한다. 탐욕 알고리즘으로 얻어진 해답은 (￠16 = ￠12 ＋ ￠1 ＋ ￠1 ＋ ￠1 ＋ ￠1) 로 동전의 개수가 5개이다. 하지만 최적의 해답은 (￠16 = ￠10 ＋ ￠5 ＋ ￠1) 으로 동전의 개수가 3개 임을 알 수 있다.

결론적으로 탐욕 알고리즘은 항상 최적의 해를 보장하지 못한다. 따라서 알고리즘으로 부터 얻은 결과가 최적의 해답인지를 반드시 검증해야 한다.

Change Problem Algorithm

Pseudocode

// Pseudocode: Change Problem
while (there are more coins and the instance is not solved)
{
    Grab the largest remaining coin; // selection procedure

    // feasibility check
    if (adding the coin makes the change exceed the amount owed)
        reject the coin;                
    else
        add the coin to the change;
    // solution check
    if (the total value of the change equals the amount owed)
        the instance is solved;
}